Apolonio PRC.

Este caso lo vamos a resolver en tres fases utilizando una inversión:

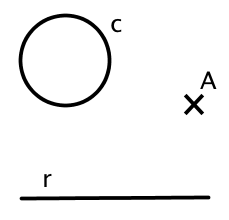
Fase 1: Invertir con centro en el punto A los elementos r y c. De esta manera r se transformará en un circunferencia c' y si utilizamos como constante de la inversión la potencia que tenga el punto A respecto de c, esta se transformará en si misma (muy cómodo).

Fase 2: Trazar las rectas tangentes (t'_n) a las circunferencias c' y r'. En el caso general habrá dos exteriores y dos interiores.

Fase 3: Invertir todos los elementos con la misma constante utilizada en la fase 1. Las inversas de c' y r', lógicamente, serán los datos iniciales c y r. Las inversas de las rectas tangentes (c₁ es la inversa de t'₁) seguirán siendo tangentes a las inversas de las circunferencias c' y r' (o sea a los datos iniciales del problema c y r). Esto se debe a que en las inversiones se mantienen los ángulos antes y después de la operación.

A pertenece a r.

Se puede definir una inversión que transforme la circunferencia c en la recta r y viceversa. Para que esto ocurra el centro de la inversión ha de estar en:

• La circunferencia (para que la circunferencia se pueda transformar en recta)
• En una perpendicular a la recta que pase por el centro de la circunferencia para que se pueda transformar una en otra.

Si la circunferencia solución debe pasar por A, su inversa pasará por A' (que se determina con la recta AO_inv1).

Este problema (AA'r) es el caso particular ya visto de PPR, donde uno de los puntos está en la recta.

La segunda solución proviene de una inversión negativa de centro O_inv2 que se resuelve como el· caso anterior.

A pertenece a c.